- Hronika
- Kolumne
-
Radio
- Izdvajamo
-
Emisije
- Dokumentarni program
- Pop top
- Europuls
- Zrno po zrno
- Radio ordinacija
- Kulturna panorama
- Zelena priča
- Epoleta
- +382
- Spona
- Svijet jednakih šansi
- Matica
- Život po mjeri čovjeka
- Link
- Izokrenuti svijet
- Koracima mladih
- Moja profesija je...
- Sportski program
- Kulturno-umjetnički program
- Muzički program
- Koracima prošlosti
- Naučno-obrazovni program
- RCG
- R98
- Programska šema
- Trofej Radija Crne Gore
- Frekvencije
- Radio drama
Nauka i tehnologija
29. 10. 2024.
11:17 >> 11:17
Čitaj mi:
BONUS PITANJE
„Nemoguć” dokaz Pitagorine teoreme objavili srednjoškolci
Ono što je počelo kao bonus pitanje na takmičenju iz matematike u srednjoj školi rezultiralo je sa zapanjujućih 10 novih načina da se dokaže drevno matematičko pravilo Pitagorine teoreme.
Dugo se tvrdilo da je nemoguće koristiti trigonometriju da se dokaže šta je zapravo teorema koja je fundamentalna za trigonometriju. Ovo spada u logičku zabludu mišljenja pokušavajući da dokaže ideju sa samom idejom.
„Ne postoje trigonometrijski dokazi jer su sve osnovne formule trigonometrije same zasnovane na istinitosti Pitagorine teoreme”, napisao je matematičar Eliša Lumis 1927. godine.
Ali, sada dvije drugarice iz srednje škole u Americi, Ne'Kiia Džekson i Kalkea Džonson, postigle su nemoguće tokom svoje posljednje godine srednje škole. One su objavile te rezultate zajedno sa još devet dokaza.
„Bilo je mnogo puta kada smo obje željele da napustimo ovaj projekat, ali smo odlučile da istrajemo i da završimo započeto”, napisale su djevojke u radu.
Pitagorina teorema opisuje odnos između tri strane pravouglog trougla. Nevjerovatno je korisna za inženjering i građevinarstvo i koristili su je ljudi vjekovima prije nego što je jednačina pripisana Pitagori, uključujući, neki tvrde, i u zgradi Stounhendža. Teorema je osnovni zakon u oblasti trigonometrije, koji u suštini izračunava odnose između stranica i uglova trouglova, a vjerovatno nema ko se ne sjeća jednačine a2+b2=c2.
„Učenici možda ne shvataju da su dvije konkurentske verzije trigonometrije utisnute u istu terminologiju”, objašnjavaju djevojke, prenosi Science Alert, dodajući da u tom slučaju, pokušaj da se shvati smisao trigonometrije može biti kao pokušaj da se shvati smisao slike na kojoj su dvije različite slike odštampane jedna na drugu. Razdvajanjem ove dvije povezane, ali različite varijacije, Džekson i Džonson su uspjeli da dođu do novih rješenja koristeći Zakon sinusa, zaobilazeći direktno kružno razmišljanje. One navode ovaj metod u svom novom radu, iako primjećuju da je granica između trigonometrijskog i netrigonometrijskog donekle subjektivna. Takođe ističu da su prema njihovoj definiciji dva druga iskusna matematičara, Zimba i Luzia, dokazali teoremu i koristeći trigonometriju, prkoseći ranijim tvrdnjama da je to nemoguće. U jednom od svojih dokaza, učenice su definiciju računanja sa trouglovima dovele do krajnosti tako što su jedan veći trougao ispunili nizovima manjih trouglova i koristeći račun da pronađu mjere stranica originalnih trouglova.
„Izgleda kao ništa što sam ikada vidio”, rekao je matematičar sa Univerziteta Konektikat Alvaro Lozano-Robledo Niku Ogasi.
U krajnjem rezultatu Džekson i Džonson pružaju jedan dokaz za pravouglove trougle koji imaju dvije jednake stranice i još četiri dokaza za pravouglove trougle sa nejednakim stranicama, ostavljajući još najmanje pet za „zainteresovanog čitaoca da otkrije”.
„Objaviti rad u tako ranom uzrastu zaista je zapanjujuće”, kaže DŽonson, koja sada studira inženjerstvo zaštite životne sredine, dok je njena koleginica upisala farmaciju.


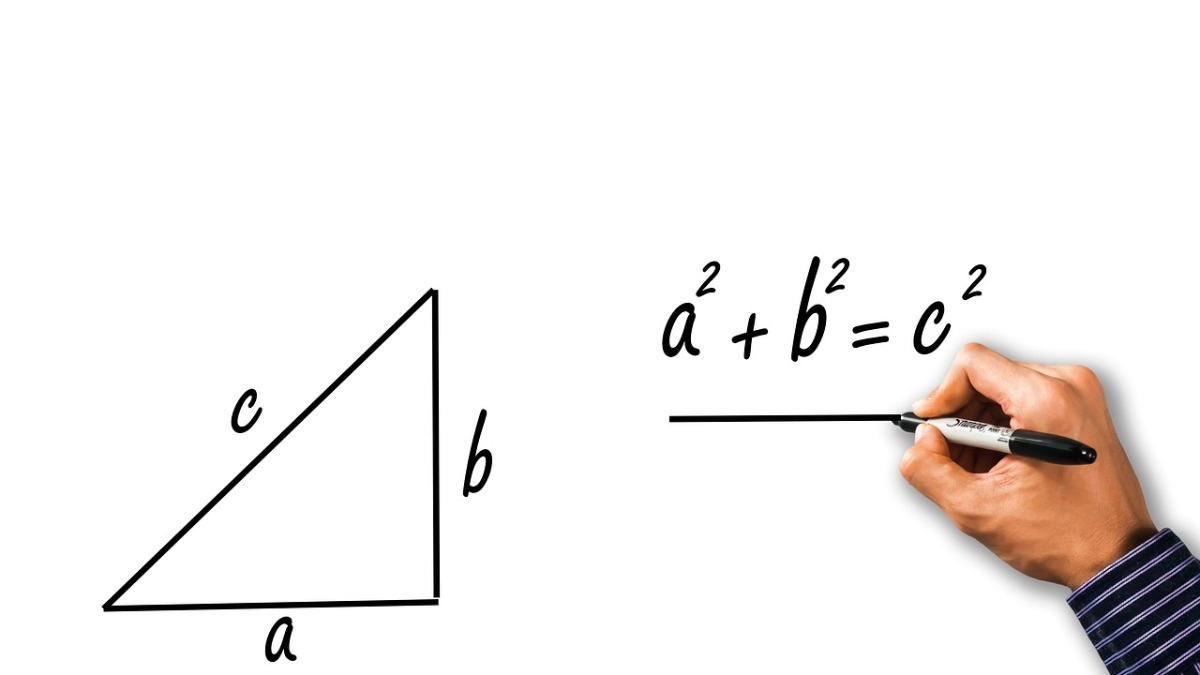
Коментари0
Остави коментар